Advantages, Disadvantages and Applications of Regula Falsi Method
Introduction
This is a very simple and old method of obtaining a real root. View the history associated with this method. In mathematics, Regula-Falsi Method False Position Method is used for solving an equation in one unknown variable. This method is trial and error because in this method we use test (false) values for the unknown variable and then adjust them according to the outcome. This method is sometimes referred to as guess and check method.Regula Falsi Method is also know as False Position Method.
Move to Advantages of Regula Falsi Method.
Move to Limitations of Regula Falsi Method or Disadvantages of Regula Falsi Method.
and Applications of regular falsi method.
Index
Graphical Representation
Here is the graphical representation of this method which is easily understandable.
Regula Falsi Method Graph
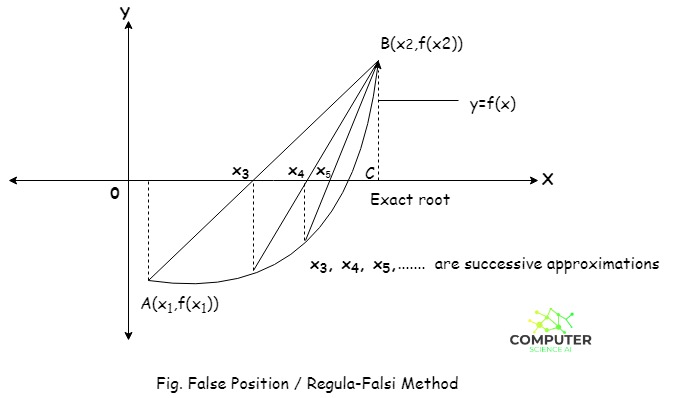
First of all we search for the points x1 and x2 such that f(x1) and f(x2) are of opposite signs so that there will lie a root of f(x)=0 between x1 and x2. Geometrically these points are A(x1,f(x1)) and B(x2,f(x2)) on the curve of y=f(x). The exact root is at C, where the curve intersects the X-axis. Now join AB. Then AB is chord. We replace the curve AB by chord AB. So that the point of intersection of chord AB with X-axis gives the first approximate position (false position) of the exact root.
Equation of chord AB in two point form is
x-x1
x1-x2
=
y-f(x1)
f(x1)-f(x2)
put y=0,
x-x1
x1-x2
=
-f(x1)
f(x1)-f(x2)
∴ x=
x1-
f(x1)(x1-x2)
f(x1)-f(x2)
∴ x3=
x1f(x1)-x1f(x2)-x1f(x1)+x2f(x1)
f(x1)-f(x2)
......(x=x3, the first approximation)
∴ x3=
x1f(x2)-x2f(x1)
f(x2)-f(x1)
......(1)
Where f(x1)f(x2)<0)
If further f(x3) and f(x2) are of opposite signs (as shown in the fig) then the root lies between x3 and x2 an we replace x1 by x2 in (1) otherwise we replace x2 by x3 and get next approximation.
Thus 1 can be generalized as the formula used for solving the equation using regula falsi method is
∴ xn+1=
xn-1f(xn)-xnf(xn-1)
f(xn)-f(xn-1)
where, f(xn-1)f(xn)<0 for each n.
That is why this method called as 'Variable Chord Method'.
Procedure for false position method to find the root of the equation f(x)=0
- Choose two initial values x1,x2 (x2>x1) such that f(x1), f(x2) are of opposite signs so that there is a root in between x1 and x2.
- Let x3 be the next approximation, now the formula ∴ x3=x1f(x2)-x2f(x1) f(x2)-f(x1)
- Find f(x3). If f(x3).f(x2) < 0 then go to step 4. Otherwise name x1 as x2 and then go to step 4.
- Calculate the next successive approximations using the formula,
∴ xn+1=xn-1f(xn)-xnf(xn-1) f(xn)-f(xn-1) - Stop this process when |xn-xn-1|<ε, where ε is the accuracy required.
Example: Regula Falsi Method
Here is the solved example on regula falsi/false position method.Problem:
Find the root lying between 1 and 2 of the equation x3-3x+1=0 upto 3 decimal places by Regula Falsi / False Position Method.Solution:
Note that we are solving for f(x)=0.f(x)=x3-3x+1 is the given equation.
f(1)=-1,f(2)=3
∴ the root lies between 1 and 2. ....f(1)f(2)<0
The first approximation is
∴ x1=
1xf(2)-2xf(1)
f(2)-f(1)
=
1x3-2x(-1)
3-(-1)
= 1.25
Now f(x1)=f(1.25)=-0.7969<0 and f(x2)=3>0
∴ root lies in (1.25,2)
The second approximation is
∴ x2=
1.25xf(2)-2xf(1.25)
f(2)-f(1.25)
=
1.25x3-2x(-0.7969)
3-(-0.7969)
= 1.4074
Now f(x2)=f(1.4074)=-0.4345<0 and f(x2)=3>0
∴ root lies in (1.25,2)
The third approximation is
∴ x3=
1.4074xf(2)-2xf(1.4074)
f(2)-f(1.4074)
=
1.4074x3-2x(-0.4345)
3-(-0.4345)
= 1.4824
Now f(x3)=f(1.4824)=-0.1896<0 and f(x2)=3>0
∴ root lies in (1.4824,2) by continuing this procedure, we get x4=1.5132, x4=1.525, x6=1.5296, x7=1.5311, x8=1.5317, x9=1.5319 ∴ the correct root = 1.532 (up to 3 decimal places)
Scilab Program For Regula-Falsi / False Position Method
Here is the source code of Scilab program for Regula-Falsi / False Position Method.
deff('y=f(x)','y=x^3-1'); // Define the function
a=0;b=2; //Determining the initial values such that f(x1)f(x2) < 0
i=1; // set counter to 1;
while(i<=15) //up to 15 iteration
c=(a*f(b)-b*f(a))/(f(b)-f(a)); // False position formula
if (f(a)*f(c)7lt;0) then
b=c;
else
a=c;
end
i=i+1;
[c,f(c)]
end
/* Output of above code:-
ans =
0.25 -0.984375
ans =
0.4657534 -0.8989659
ans =
0.640363 -0.7374097
ans =
0.7699425 -0.5435693
ans =
0.8585771 -0.3670959
ans =
0.9154532 -0.2328002
ans =
0.9503612 -0.1416466
ans =
0.9711796 -0.0839932
ans =
0.9833781 -0.0490414
ans =
0.9904509 -0.0283745
ans =
0.9945266 -0.0163304
ans =
0.9968668 -0.00937
ans =
0.9982078 -0.0053669
ans =
0.9989753 -0.0030709
ans =
0.9994143 -0.0017562
*/
Conclusion from Scilab Program for False Position Method
As we increase the number of iterations we get more accurate values of root. Regula Falsi Method program in other programming languages C++ Program for Regula Falsi MethodJava Program for Regula Falsi Method
Python Program for Regula Falsi Method
Advantages
- It does not require the derivative calculation.
- This method has first order rate of convergence i.e. it is linearly convergent. It always converges.
Disadvantages
Following are the limitations of regula falsi method- As it is trial and error method in some cases it may take large time span to calculate the correct root and thereby slowing down the process.
- It is used to calculate only a single unknown in the equation.
You might want to check out newton raphson method and lagrange's interpolation method.
Applications
- The Regula Falsi method is applied to prediction of trace quantities of air pollutants produced by combustion reactions such as those found in industrial point sources.
(source: wiki)
Examples For Practice
Here are some examples for practice on regula-falsi / false position method.- Find a real root of x3-9x+2=0 up to 3 decimal places by regula-false method.
- Find the positive root of x2-log10x-10=0 by false position method.
- Find the root of the equation ex-2x=0 which lies between 0 and 1.
- Find the real root of the equation xex-1=0, using Regula-falsi method, correct up to 3 decimal places.